Model-Free Adaptive (MFA)
Control
Concept and Significance of Model-Free Adaptive
Control
A Model-Free Adaptive control system has the following
properties or features:
• No precise quantitative knowledge of the process
is available;
• No process identification mechanism or identifier
is included in the system;
• No controller design for a specific process
is needed;
• No complicated manual tuning of controller parameters
is required; and
• Stability analysis criteria are available to
guarantee the closed-loop system stability.
The essence of MFA control is described with discussions
relating to combustion process control on the following
five issues:
Process Knowledge Issue
Most advanced control methods are based on a good understanding
of the process and its environment. Laplace transfer
functions or differential equations are used to represent
the process dynamics. In many process control applications,
however, the dynamics may be too complex or the physical
process is not well understood. Quantitative knowledge
of the process is then not available. This is called
a “black box” problem.
In many cases, we may have some knowledge of the process
but are not sure if the knowledge is accurate or not.
In process control including combustion control applications,
we often deal with raw materials, wild inflows, changing
fuel type and heating values, unpredictable downstream
demand changes, and frequent switches of product size,
recipe, batch, and loads. These all lead to a common
problem: that is, we are not sure if the process knowledge
is accurate or not. This is called a “gray box”
problem.
If quantitative knowledge of the process is available,
we have a “white box” to deal with. It is
a relatively simple task to design a controller for
the process in this case because we can use well-established
control methods and tools.
Although Model-Free Adaptive control can actually deal
with black, gray, and white box problems, it is more
suitable to deal with the gray box problem. Most industrial
processes are gray boxes.
Process Identification Issue
For traditional adaptive control methods, if the quantitative
knowledge of the process is not available, an on-line
or off-line identifier is required to obtain the process
dynamics. This contributes to a number of fundamental
problems:
• the headache of off-line training that might
be required,
• the tradeoff between the persistent excitation
of signals for correct identification and the steady
system response for control performance,
• the model convergence and local minimum problems,
and
• the system stability issues.
The main reason that identification-based control methods
are not well suited to process control is that control
and identification are always in conflict. Good control
will lead to a steady state where setpoint (SP), controller
output (OP), and process variable (PV) will show straight
lines on a trend chart. Since any stable system can
reach a steady state where process dynamic changes cannot
be seen, good identification may require insertion of
test signals. This requirement is not easily accepted
by plant operators.
MFA control avoids the fundamental problems by not using
any identification mechanism in the system. Once an
MFA controller is launched, it will take over control
immediately. The MFA algorithms used to update the weighting
factors are based on a sole objective, which is to minimize
the error between SP and PV. That means, when the process
is in a steady state where error is close to zero, there
is no need to update the MFA weighting factors.
Controller Design Issue
The main reason PID is still popular is that it is a
general-purpose controller that does not require controller
design procedures. Designing a controller for a specific
application requires special expertise. Since most advanced
controllers are model-based, they cannot be a general-purpose
controller. Thus, they are not widely used in process
control, although these methods have been developed
for 30 to 40 years.
MFA controllers are general-purpose controllers. A number
of MFA controllers have been developed to control a
variety of problematic industrial loops. Examples include
SISO MFA to replace PID and requires no manual tuning,
Nonlinear MFA to control extremely nonlinear processes,
Anti-delay MFA to control processes with large time
delays; MIMO MFA to control multivariable processes;
Feedforward MFA to deal with large measurable disturbances;
and Robust MFA to force the process variable to stay
within defined bounds.
For an MFA controller user, there are no controller
design procedures required. One can simply select the
appropriate controller as its name suggests, configure
the controller with certain parameters and launch the
MFA controller. This is one of the major differences
between a Model-Free Adaptive controller and other model-based
advanced controllers.
Controller Parameter Tuning Issue
An adaptive controller should not need to be manually
tuned. This is also true for MFA controllers. MFA can
adapt to new operating conditions due to changes in
process dynamics, loads, or disturbances, and there
is no manual tuning required. As a user-friendly feature,
certain parameters are available to allow the user to
quickly adjust the control performance.
System Stability Issue
Control system stability analysis is always an important
issue because it determines if the controller will be
useful in practice. When the system stability criterion
is available, one can use the criterion to decide if
the control system can be safely put in operation. As
shown in Figure 1, a model-based self-tuning adaptive
control system has 3 major components: controller, process,
and model. Here, the model refers to a mathematical representation
describing the relationship between the process input
and output. The model is usually built by an identifier
that has a learning algorithm to minimize the model
error em(t) (the difference between PV and model output
y2(t) ) using the process input and output data.
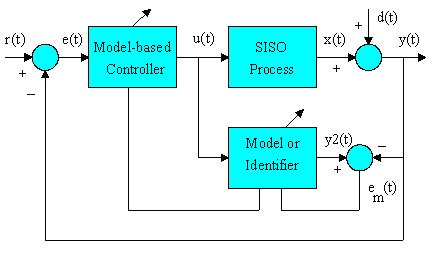 |
Signals:
r(t) – Setpoint
u(t) – Controller Output
y(t) – Process Variable
x(t) – Process Output
d(t) – Disturbances
e(t) – Error
e(t) = r(t) - y(t).
y2(t) – Model Output
em(t) – Model Error
em(t) = y2(t) - y(t).
|
Figure 1. Model-Based Adaptive
Control System
Then, the stability of the overall closed-loop
control system is related to the process, the controller,
and the model in the following way:
• stability of the process is assumed (i.e.,
the process is open-loop stable);
• stability of the control loop must be guaranteed
by the convergence of the model; but
• convergence of the model is dependent on the
stability and persistent excitation of signals originating
from the control loop.
This is a circular argument that it is difficult to
resolve. Thus, there is no general stability criterion
available for a model-based adaptive control system.
In other words, each time a model-based adaptive controller
is used in a control system, its stability has to
be analyzed. This is certainly a major technical barrier
in applying model-based adaptive control methods.
In contrast, since MFA does not have an identifier,
a general system stability criterion is developed.
That is, if the process is passive (a process that
does not generate energy or heat by itself), the closed-loop
MFA control system stability is guaranteed, and the
process can be linear/nonlinear, time invariant/time-varying,
etc. A combustion process is a passive process since
the heat it generates has to come from burning fuel
from outside of the process.
Single-Loop MFA Control System Structure
The system structure of a single-input-single-output
(SISO) MFA control system is shown in Figure 2. The
structure is as simple as a traditional single-loop
control system that includes a SISO process, a SISO
MFA controller, and a feedback loop.
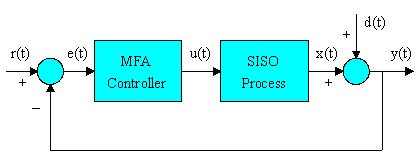 |
Signals:
r(t) – Setpoint, SP
u(t) – Controller Output, OP
y(t) – Process Variable, PV
x(t) – Process Output
d(t) – Disturbances
e(t) – Error, e(t)=r(t)-y(t).
|
Figure 2. Single-Loop MFA Control System
Control Objective
The control objective for the controller is to produce
an output u(t) to force the process variable y(t)
to track the given trajectory of its setpoint r(t)
under variations of setpoint, disturbances, and process
dynamics. In other words, the task of the MFA controller
is to minimize the error e(t) in an online fashion.
The minimization of e(t) is achieved by (i) the regulatory
control capability of the MFA controller, and (ii)
the adjustment of the MFA controller weighting factors
that allow the controller to deal with process dynamic
changes, disturbances, and other uncertainties.
Compared to Figure 1, the MFA system does not have
a process model or identifier. Thus, no model error
em(t) needs to be minimized and only the error e(t)
between the setpoint (r(t) or SP) and process variable
(y(t) or PV) needs to be minimized.
MFA Controller Architecture
Figure 3 illustrates the core architec¬ture of
a SISO MFA controller. Used as a key component, a
multilayer perceptron neural network consists of one
input layer, one hidden layer with N neurons, and
one output layer with one neuron.
Within the neural network there is a group of weighting
factors (wij and hi) that can be updated as needed
to vary the behavior of the controller. The algorithm
for updating the weighting factors is based on the
goal of minimizing the error e(t). Since this effort
is the same as the control objective, the adaptation
of the weighting factors can assist the controller
in minimizing the error while process dynamics are
changing.
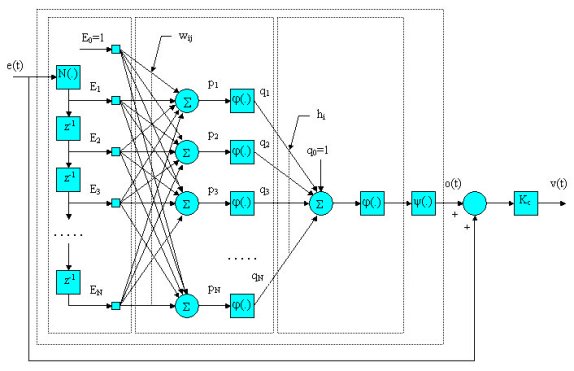
Figure 3. Architecture of a SISO MFA controller
Also, the neural network based MFA controller
“remembers” a portion of the process data
providing valuable information for the process dynamics.
In comparison, a digital version of the PID remembers
only the current and previous two samples. In this
regard, PID has almost no memory, and MFA possesses
the memory that is essential to a “smart”
controller.
MFA Control System Requirements
As a feedback control system, MFA requires that the
process be
• controllable,
• open-loop stable, and
• either direct or reverse acting (process does
not change signs).
If the process is not controllable, improvement of
the process structure or its variable pairing is required.
If the process is not open-loop stable, it is always
a good practice to stabilize it first. However, for
certain simple open-loop unstable processes such as
a non self-regulating level loop, no special treatment
is required when using MFA.
If a process changes its sign within its operating
range, special MFA controllers are required. MFA controllers
can be easily configured with only a few parameters.
|