Multivariable MFA
Control System
In control applications, most processes have multiple
inputs and multiple outputs with interactions in between.
The level and density loops of an evaporator, and the
temperature loops of a multi-zoned furnace are good
examples of multivariable processes. Lacking general-purpose
multivariable controllers, a large percentage of multivariable
processes are treated as single variable processes resulting
in poor control, wasted energy and materials, inconsistent
quality, and plant upsets.
This graph illustrates a multivariable Model-Free Adaptive
(MFA) control system, which consists of a multi-input
multi-output (MIMO) process and an MIMO MFA controller.
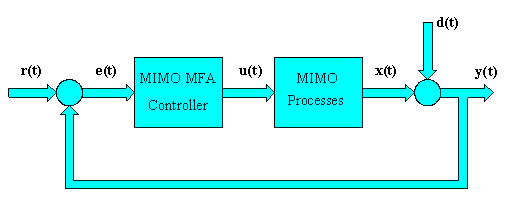
Multivariable MFA control system
Similar to a SISO system, the MIMO system has controller
setpoints r(t), error signals e(t),
controller outputs u(t), process variables
y(t), and disturbance signals d(t).
Since it is a multivariable system, all the signals
here are vectors represented in bold case.
2-Input-2-Output MFA Control System
Without losing generality, we will show how a MIMO MFA
controller works with a 2-input-2-output (2x2) system
as illustrated in following graph. In the 2x2 MFA system,
the 2x2 MFA controller consists of two main controllers
C11, C22, and two compensators C21, and C12. The process
has four sub-processes G11, G21, G12, and G22.
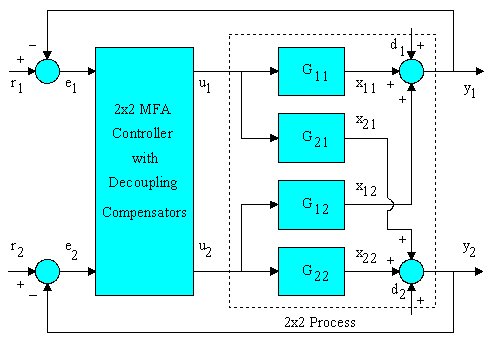
2-input-2-output MFA control system
The measured process variables y1 and y2 are used
as the feedback signals for the main control loops.
They are compared with the setpoints r1 and r2 to produce
errors e1 and e2. The output of each controller associated
with one of the inputs e1 or e2 is combined with the
output of the compensator associated with the other
input to produce control signals u1 and u2. The output
of each sub-process is cross-added to produce measured
process variables y1 and y2. Notice that in real applications
the outputs from the sub-processes are not measurable
and only their combined signals y1 and y2 can be measured.
Thus, by the nature of the 2x2 process, the inputs u1
and u2 to the process are interconnected with outputs
y1 and y2. The change in one input will cause both outputs
to change.
The control objective for this 2x2 MFA control system
is to produce control outputs u1(t) and u2(t) to force
the process variables y1(t) and y2(t) to track their
setpoints r1(t) and r2(t), respectively. The minimization
of e1(t) and e2(t) is achieved by (i) the regulatory
control capability of the MFA controllers, (ii) the
decoupling capability of the MFA compensators, and (iii)
the adjustment of the MFA weighting factors that allow
the controllers to deal with the dynamic changes, large
disturbances, and other uncertainties.
2x2 MFA Controller Configuration
A 2x2 MFA controller can be considered to have 2 main
controllers C11 and C22. For each main controller, the
parameters to configure are: (1) Sample Interval, Ts
- the interval between two samples or calculations in
seconds. A high speed MFA controller can run at a 1
millisecond rate; (2) Controller Gain, Kc1 - use of
a default value is recommended, (3) Time Constant, Tc
- a rough estimate of the process Time Constant in seconds;
(4) Acting Type - direct or reverse acting of the process;
and (5) Compensator Gain, Kc2 - to deal with the interaction
from the other loop.
MIMO MFA Controller Application Guide
A MIMO system can be much more complex than a SISO system,
therefore precautious must be taken when applying a
MIMO MFA controller. When designing a multivariable
control system, the first step is to decide which process
variable is paired with a manipulated variable. A MIMO
MFA control system should follow these pairing rules:
(1) Each main process (G11, G22) has to be controllable,
open-loop stable, and either reverse or direct acting;
(2) A process with a large static gain should be included
in the main loop as the main process (G11, G22), and
a process with a small static gain should be treated
as a sub-process. (G21, G12); (3) A faster process should
be paired as the main process, and a slower process
or processes with time delays should be treated as sub-processes;
and (4) If Pairing Rules 2 and 3 are in conflict, a
tradeoff is the only option.
As a general guide, an MFA control system should be
designed based on the degree of interactions between
the loops. This table lists the control system design
strategy based on the degree of interaction of a MIMO
process.
MFA control system design strategy
|
Interaction Measure |
Control
Strategy |
| Small to non interaction |
Tighten both loops with SISO MFA. |
| Moderate interaction |
Tighten important loops with SISO MFA and de-tune
less important loops; or Use MIMO MFA for better
overall control. |
| Severe interaction |
Use MIMO MFA to control the process. May need
to de-tune less important loops. |
|